A Dozen Notes, Give or Take

Introduction

Western classical music typically uses twelve distinct notes: C, C#, D, D#, E, F, F#, G, G#, A, A#, B. After this, you hit an octave and repeat.

It always bugged me: why twelve?

Here I try to provide an answer with a few rules and a few graphs. This is a little hand wavy, I'm sure that it's not original, and I know someone who knows more could make this more convincing and more rigorous.

But this is the internet. Who cares?

Exposition

We're going to examine systems with various numbers of notes, but first we're going to set a few ground rules for our exploration:

1. We want our notes to form an even progression. To be precise, we want the ratio between two consecutive notes to be constant. This is called an equal temperament, and will mean that our set of notes won't favor any particular key.
2. With our set of notes, we want to be able to represent the harmonics of any given fundamental tone as closely as possible. When a tone is played on an instrument, the harmonics of that tone are usually present in some mixture—the exact mixture has a lot to do with the instrument's timbre. It turns out that rule (1) makes it impossible to be perfect, but since harmonics show up naturally, we want to be close.
3. We'll treat one class of harmonics with extra care: octaves. We'll insist that that we evenly divide the octave. Together with (1), this means that every time we reach an octave our notes will repeat with double the frequency.

None of these ground rules mandate 12 notes; we want that to emerge.

To drive this, I wrote a simple python script that produces some working data for middle C (261.626 Hz). Basically, this pre-computes the best-fit notes for each harmonic of middle C given different numbers of notes in the scale. The choice of C is arbitrary: picking a different fundamental would leave all of the relations intact, and would just shift the frequencies up or down a bit.

To get our feet wet with the data, let's look at the 12-tone scale we're used to, and see how its best-fit notes line up against the harmonic progression starting with middle C:

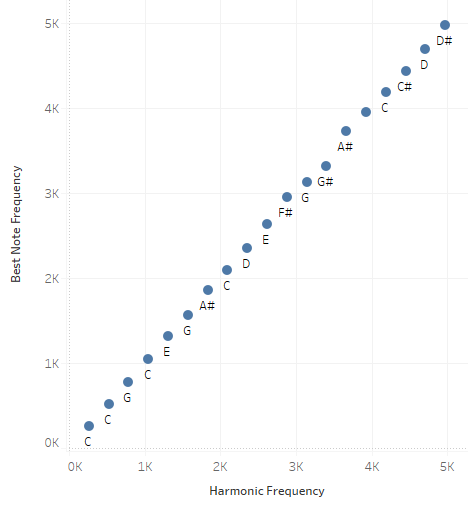
Ideally, these points would all lie on a line, since the best-fit note would exactly match its corresponding harmonic. It should be pretty clear from the plot that these don't quite lie on a line, although the lowest notes look pretty close. We can better see what's going on if we simply subtract each harmonic out from the best-fit note:

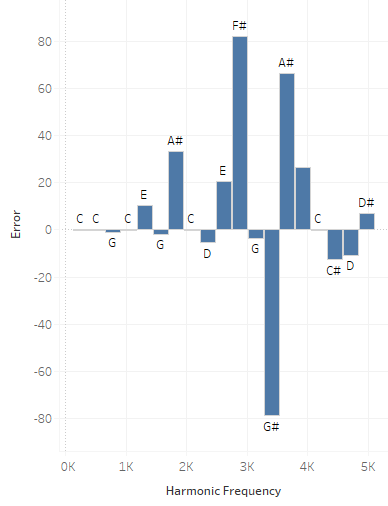
The first thing you'll notice from this plot is that the octaves (all those Cs) have no error; this is simply by design. You can also see that the third tone (G, which corresponds to a perfect fifth) is slightly flat, whereas the fifth tone (E, which corresponds to a major third) is a bit sharp. Both of these are well-known byproducts of an equal-tempered twelve-tone scale.

Beyond these notes, things seem to get pretty bad. But we're looking at the raw deviation. Instead, we're going to weight the errors, decaying them exponentially as the harmonics increase. It's a little hand wavy, but we'll defend this on the simple grounds that we expect the lower harmonics to be more important.

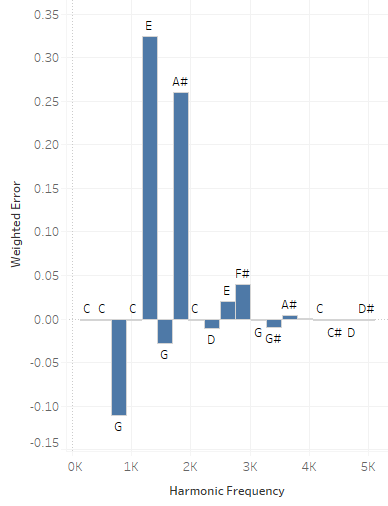
If we look at this weighted error, things look rather worse for our low-numbered harmonics, but this is just emphasizing what we think is important.

Development

Now that we've seen how well (or poorly) twelve notes perform, we can ask how well other divisions would work. For starters, let's take a look at twelve's neighbors: eleven and thirteen:

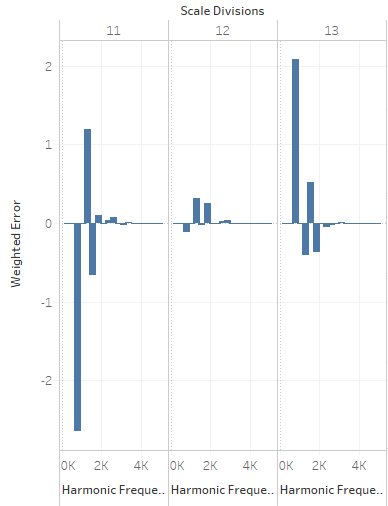
Compared to its neighbors, twelve divisions is starting to look pretty good.

To get the full picture, we'll sum the absolute value of all of the errors for each note. By plotting this total weighted error against the number of notes, we can see the overall pattern:

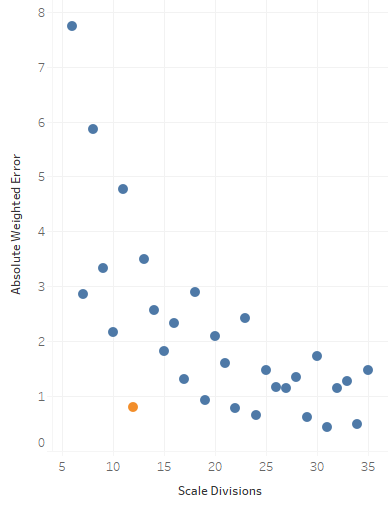
Here I've highlighted twelve just so we can see it. Two things seem immediately evident from this plot:

1. Although the error jumps around a bit, there is a clear downward trend. This shouldn't be surprising: as we add more notes, we're more likely to get one close to any given harmonic. In particular, doubling the number of notes must make things better, since the new collection is a superset of the old.
2. Twelve really does have a low error. In fact, with our error measure, you don't do better until you get to 22—and that's a lot of notes.

We can emphasize just how well twelve does by multiplying the number of notes by the error. We'll call this the efficiency of the set; roughly speaking, a set of notes is more efficient if it achieves less error with fewer notes.

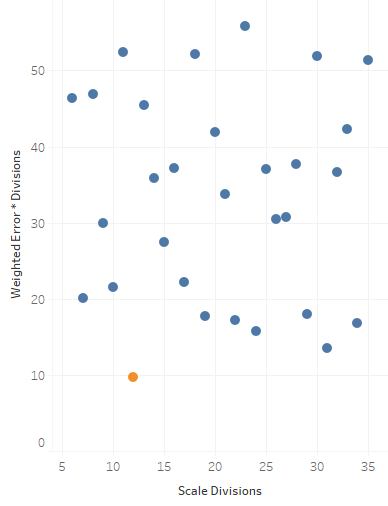
I hope it's not just for show, but twelve really does look good now.

Recapitulation

What have we learned?

It's certainly not definitive, but if harmonics of notes sound good, and we're looking for a simple set of evenly-spaced notes that approximates them well, it's hard to pick a better number of divisions than 12.

I don't know when exactly the twelve-tone scale was developed, but whoever developed it certainly didn't do this kind of analysis. We can, however, assume is that its evolution was guided by what sounded right, and I think this analysis helps shine some light on why this arrangement might be the product of that evolution.

Coda

But that's not all!

If you want to go down the rabbit hole, here are two bunnies to follow:

• You can relax our ground rule number 1: that notes need to follow an even progression. Equal temperament is actually relatively modern, and there are a slew of systems that don't satisfy this rule: just intonation, meantone temperament, Pythagorean tuning, etc. Bach's Well-Tempered Clavier was meant to be played with a well temperament, and string players will often deviate from equal temperament to better hit the overtones discussed here.
• And while twelve works out pretty well, microtonal music—dividing the octave more finely than twelve—has a history, even within the western classical domain. I haven't heard too many recordings of classical microtonal music, but I did find this recording of some of Ives' pieces for quarter-tone (24-tone) piano.

If you have a favorite recording that bends these rules, please share! And if you're interested, all the vizzes I used here are available on Tableau Public.