When using Tableau, taking an extract is always better than using a live query, right?
Well, no.
Of course. Obviously, when your data are changing and you want to get all of the latest updates in your viz, you'll want to use a live query. But if that's not the case, then an extract is clearly better, especially with Hyper in 10.5, right?
Well, no!
Shoot! This is complicated? When will live beat an extract? Let's take a look at a few cases.
A Few Basics
To understand what's going on, you should have a basic understanding of how live and extracted data sources are used by the system. If you feel a bit shaky here, I'd recommend my previous post on live vs extracts. But in a nutshell:
- When you're using an extract, the query defined by the data source is run and the whole resulting table is persisted in either a TDE (in Tableau 10.4 or before) or a Hyper database (in 10.5 and later). The queries produced by your workbook are then run against this table.
- When you're running live, the queries from your workbook are composed with the data source query. In simple cases, at least, this will result in a single query that is pushed down to the target database system, and only the results needed for the viz are returned.
We're going to look at a few cases where live can do better than an extract. As we look at them, pay particular attention to:
- The time to run the remote query,
- The time to transfer the data, and
- The time to run the local query.
These aren't rigorous perf numbers, but to give you a sense of scale, here's my setup:
- Tableau 10.5 (with Hyper) running on a i5-2500 with 8GB of RAM.
- SQL Server 2017 Express Edition running on an i7-3770 with 16GB of RAM.
- All wired together over gigabit Ethernet.
So nothing too grand. In any case, the lessons here should carry over to other hardware.
The data set is a stock history set from Kaggle that records daily stats for large number of stocks and ETFs. The schema looks like:
history(ticker, type, date, open, high, low, close, volume, openInt)
Loaded into SQL Server and indexed on (ticker, date), this results in 17.4M rows and about 1.5GB of storage. (I have no idea what the provenance or accuracy of these data are, but for this work only the size is relevant.)
Let's try to beat an extract!
Nail The Index
Let's start with an easy case: let's find the yearly average close for Tableau's stock. I'll drag the ticker into filters, years into columns, and Avg(Close) into rows. It's an award-worthy viz:
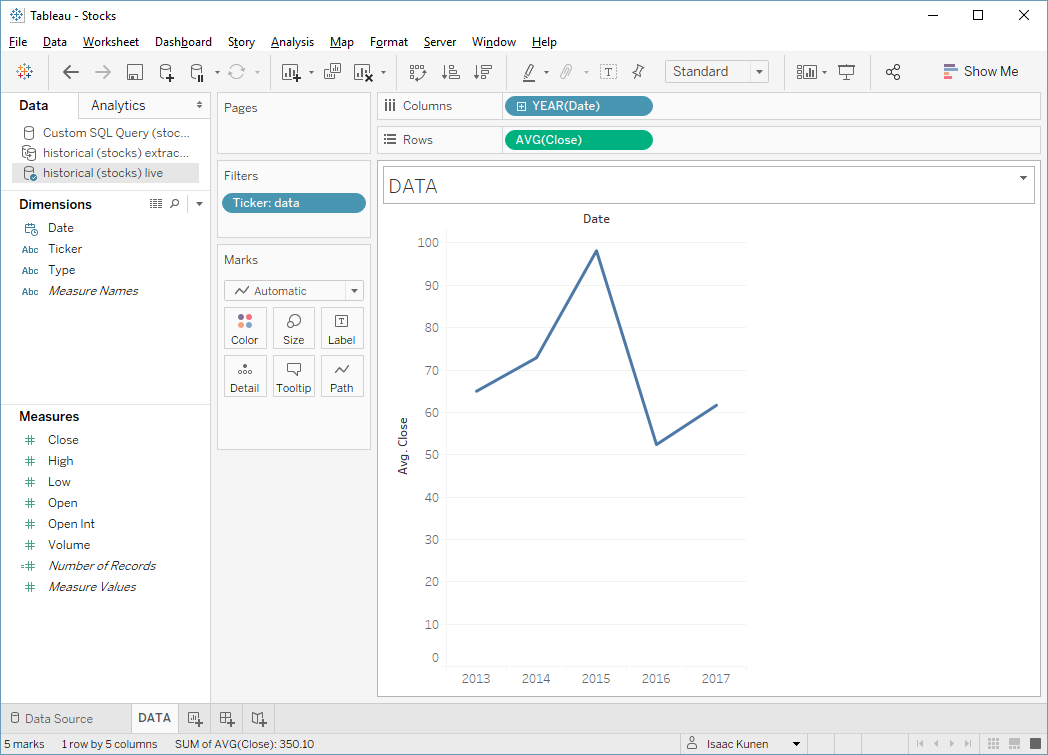
This is also an almost ideal query for our SQL Server database: it makes excellent use of the index, so the query is exceptionally fast to run; and because the aggregation happens remotely, there are almost no results to send over the wire. By looking in the log, I find that it takes a whole 0.006 seconds to run this query and fetch the results. How can we possibly beat that?
Indeed, if we recreate the same viz with an extract, Hyper takes more like 0.2 seconds to compute the viz.
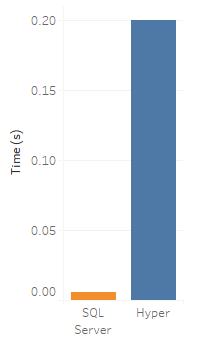
So SQL Server is faster than Hyper? Well, in this case it is, but we've almost cheated by practically tuning it to answer this query quickly. Hyper, on the other hand, doesn't require (and doesn't allow) us to tune its setup. So we're comparing the best case for SQL Server to a case for Hyper.
But the lesson is still sound: if your query (a) lines up well with the setup of your remote database, and (b) transfers very little data, then we can actually beat a Hyper extract.
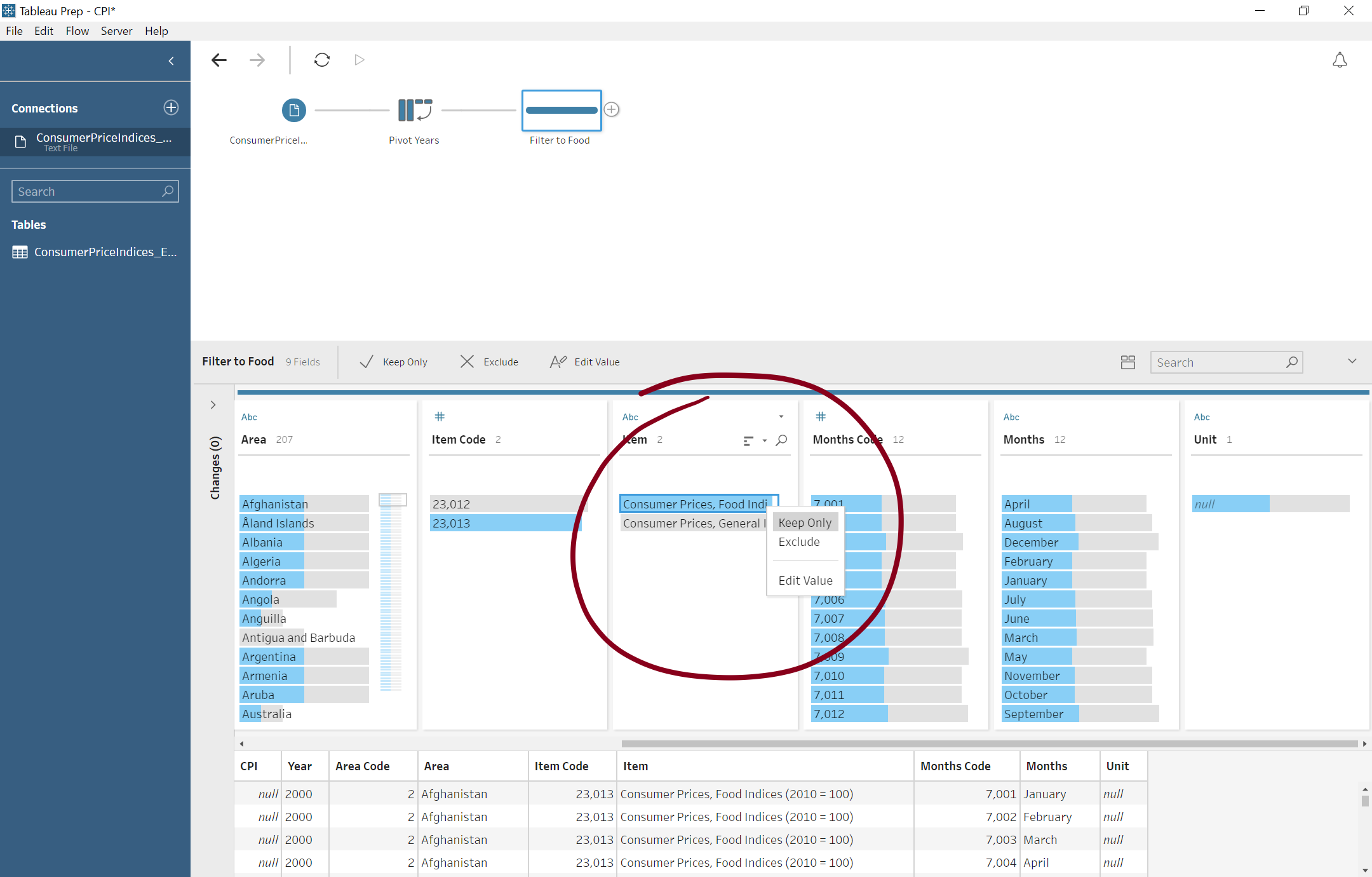
Be Truly Ad Hoc
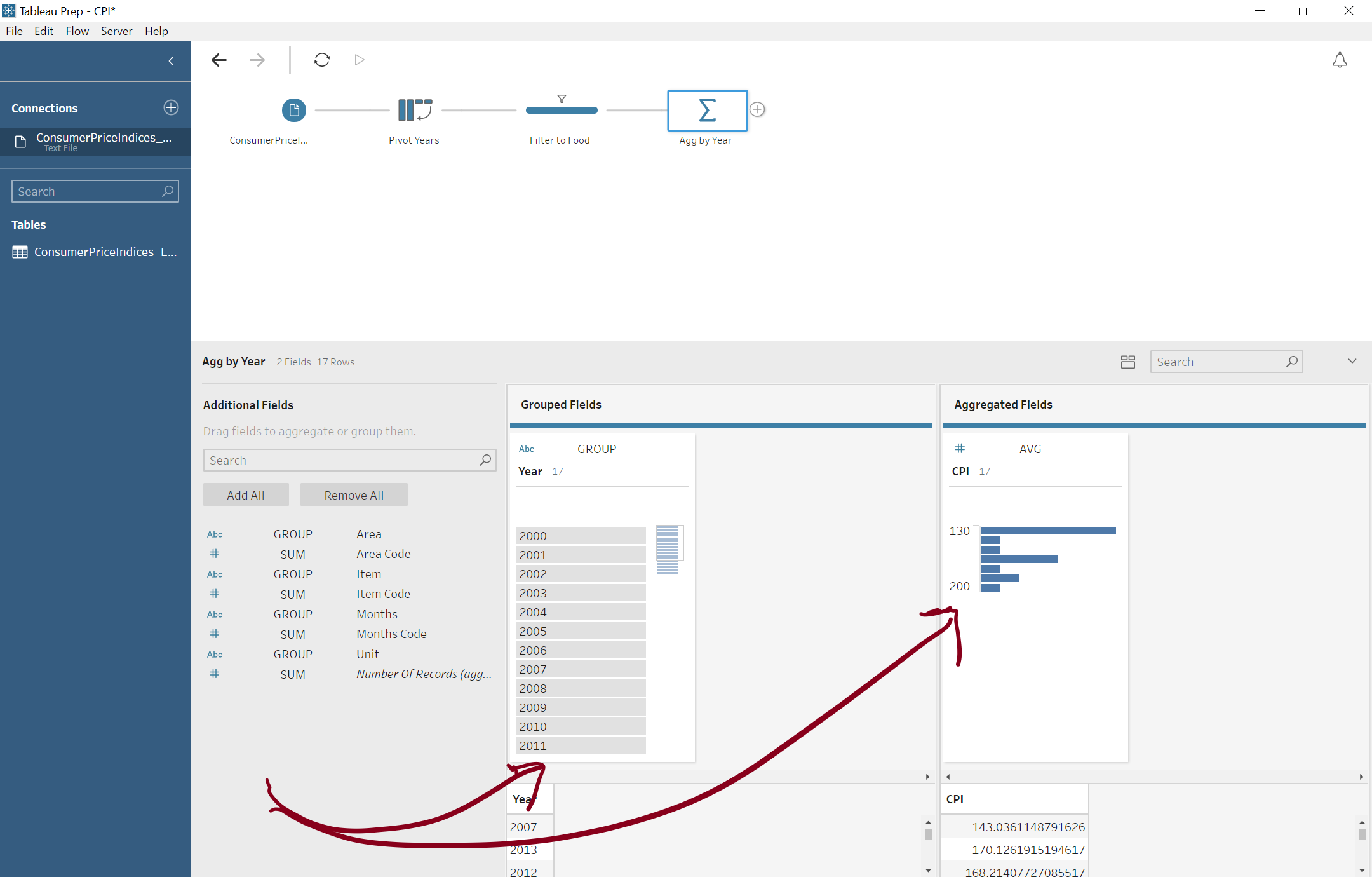
Let's try to avoid pandering to SQL Server quite so much and just ask for the number of records my data set has each year:
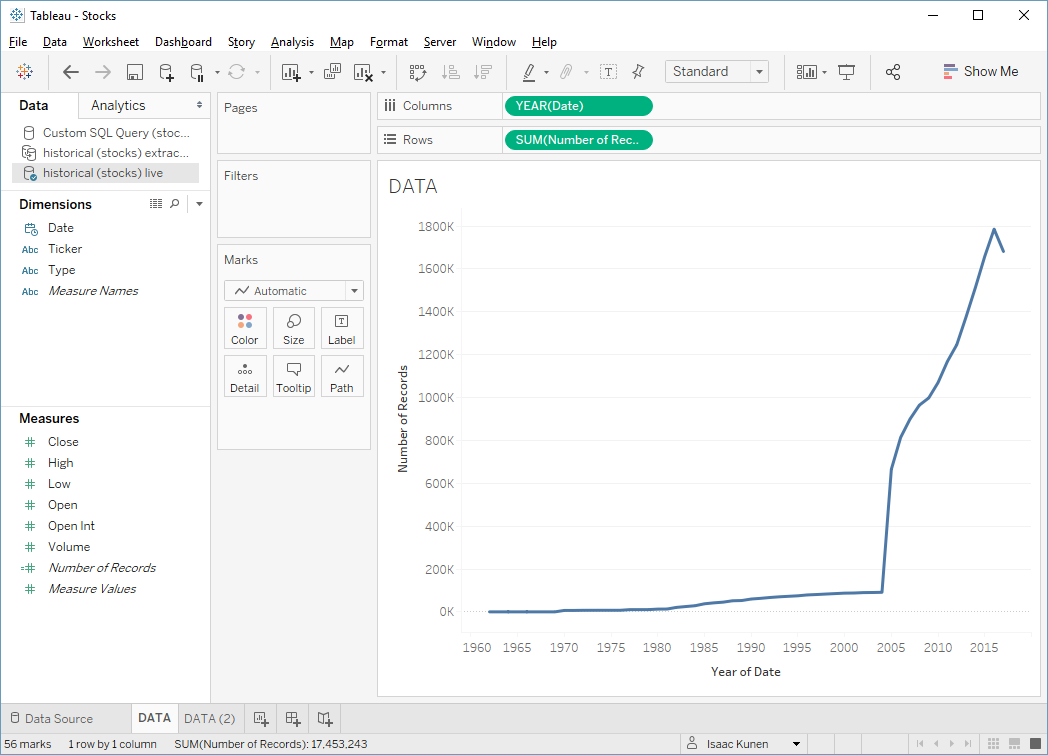
Now SQL Server takes a bit longer: 5.53 seconds. Trying this against the extract shows what Hyper can do: 0.193 seconds. In this case, both engines have to do roughly the same amount of work, but with it's column-based, in-memory execution, Hyper is the clear winner!
Except that we haven't taken into account the cost of generating the extract. When we refresh it, we find that it takes us 67.8 seconds to generate a 435MB extract. If we add that in, SQL Server starts looking pretty good:
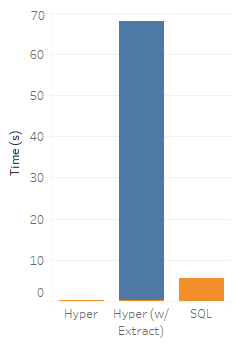
Applying a little algebra, that means that to recoup the cost of our extract, we'd need to run our viz query a hair over 15 times. Often times this will be worth it, but if the query is truly one off, I'd rather spend 5.53 seconds than 68.
Blow Up the Extract
Let's try something more horrible. Let's say that in addition to the historical stock prices, we have a table of customer holdings. We'll keep it simple; our customers have static holdings that look like:
customerholdings(customer, ticker, amount)
(I don't actually have any customers, so I randomly generated 20 holdings for each of 20,000 imaginary customers.)
We want to do things like look at the total value of all customers' holdings over time, so we join the holdings to the price history.
We then create a calc to compute the value each customer's holdings and make a viz:
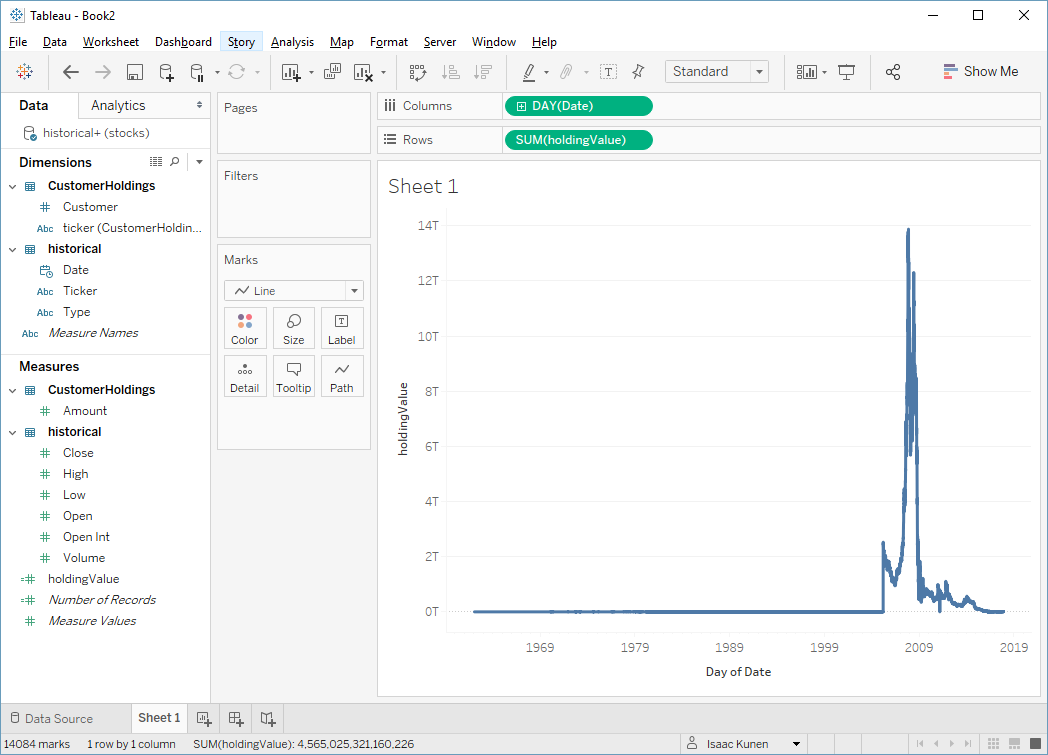
In case you're interested, that giant spike is caused by a few odd stocks like DryShips Inc. (DRYS), which somehow peaked at $1,442,048,636.45 in 2007. I don't comprehend. The graph looks funny, but again, this doesn't matter for our analysis.
What we care about is that this query takes 133 seconds to run—it's a fair bit of work for SQL Server to do. How about the extract?
Well, let's do a little back of the envelope computation. If we execute the full join in SQL Server and don't aggregate anything down, instead of the 17 million records in our history table, the result set will have about 441 million records. And these records are larger than the history rows because they have customer information as well.
Optimistically, this will end up being something like 10 gigabytes of data that I have to move over the wire, and store in a local extract. And that's all before I even get to ask my query. So unless I'm doing this a lot, I'm simply not going to bother.
Wrapping Up
So we've seen a few cases where live queries may be preferable to extracts, leaving aside the obvious cases where you simply want the most current data.
One thing we didn't talk about is federated queries: queries that span multiple data sources. As a general rule, federation makes extracts look better relative to live, because live starts to look worse. Live works best when the engine can push operations that reduce data volumes off to the remote system—operations like aggregations and filters—and federation tends to interfere with that pushdown.
But that's another ball of wax. I'll write more on federation soon.
]]>











 Go ahead and tweak the parameters to find the eyepiece you're looking for. Some details on how I built it are below the fold.
Go ahead and tweak the parameters to find the eyepiece you're looking for. Some details on how I built it are below the fold.